
Catch 'Em All: Unlocking the Secrets of the Coupon Collector's Problem
This problem is called the Coupon Collector’s Problem!

Simple approach to the problem
To simplify the approach to the problem, let’s say that we are collecting monsters, and we are getting these monsters from “surprise boxes”. For now we’ll assume that there are 100 different monsters with the same probability of getting all of them.
It is your first opening of a box. The probability of getting a new monster is … well 1, as you have no other monsters. For your second opening of a box, the probability of getting a new different one is 99/100. Indeed, there is a slight “chance” (or bad luck) of 1/100 that you’ll get the same monster as your first opening.
To generalize our finding, if we already have k different monsters, the probability of getting a new monster out of a pool of N monsters (in our case N = 100) is:
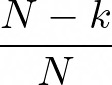
- If we already have 99 monsters, the probability of finding a new one (the ultimate one!) is 1/100
This follows a geometric distribution with parameter (𝑁−𝑘)/𝑁. The expectation of this geometric distribution is 𝑁/(𝑁−𝑘). We can interpret this expectation as:
After already having k different monsters, we’d need to open on average N/(N-k) boxes to get a new one.
- So if we already have 99 monsters, we’d need on average to open 100 boxes to have a new one.
Let’s use this expectation formula. If we have 0 monsters, the number of box openings to get a new one is:
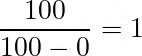
Once we have 1 monster, the number of box openings on average to get a new one is:
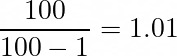
Summing both, the average number of box openings to get 2 monsters is 2.01. As we’ve seen before, there is a slight chance that we’ll get the same monster after the 2 box openings.
Generalizing, in order to get k different monsters, we’ll need to open this amount of boxes:
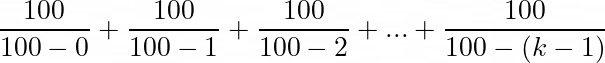
Which we can also write:
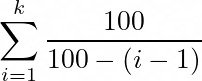
Let’s compute this sum on Python.
Show code
import numpy as np
import matplotlib.pyplot as plt
#We can build the sum with a for loop
N = 100
def openbox_depending_on_monster(k):
total = 0
for i in range(1, k + 1):
total += N / (N - (i - 1))
return total
#or with a vectorized approach
def openbox_depending_on_monster_np(k):
# np.arange creates an array starting from 1 up to k
indices = np.arange(1, k + 1)
# Directly compute the terms using vectorized operations and compute the sum
total = np.sum(N / (N - (indices - 1)))
return total
print("So to get 95% of the monsters (95) we'd need to open {} boxes".format(int(openbox_depending_on_monster_np(95))))
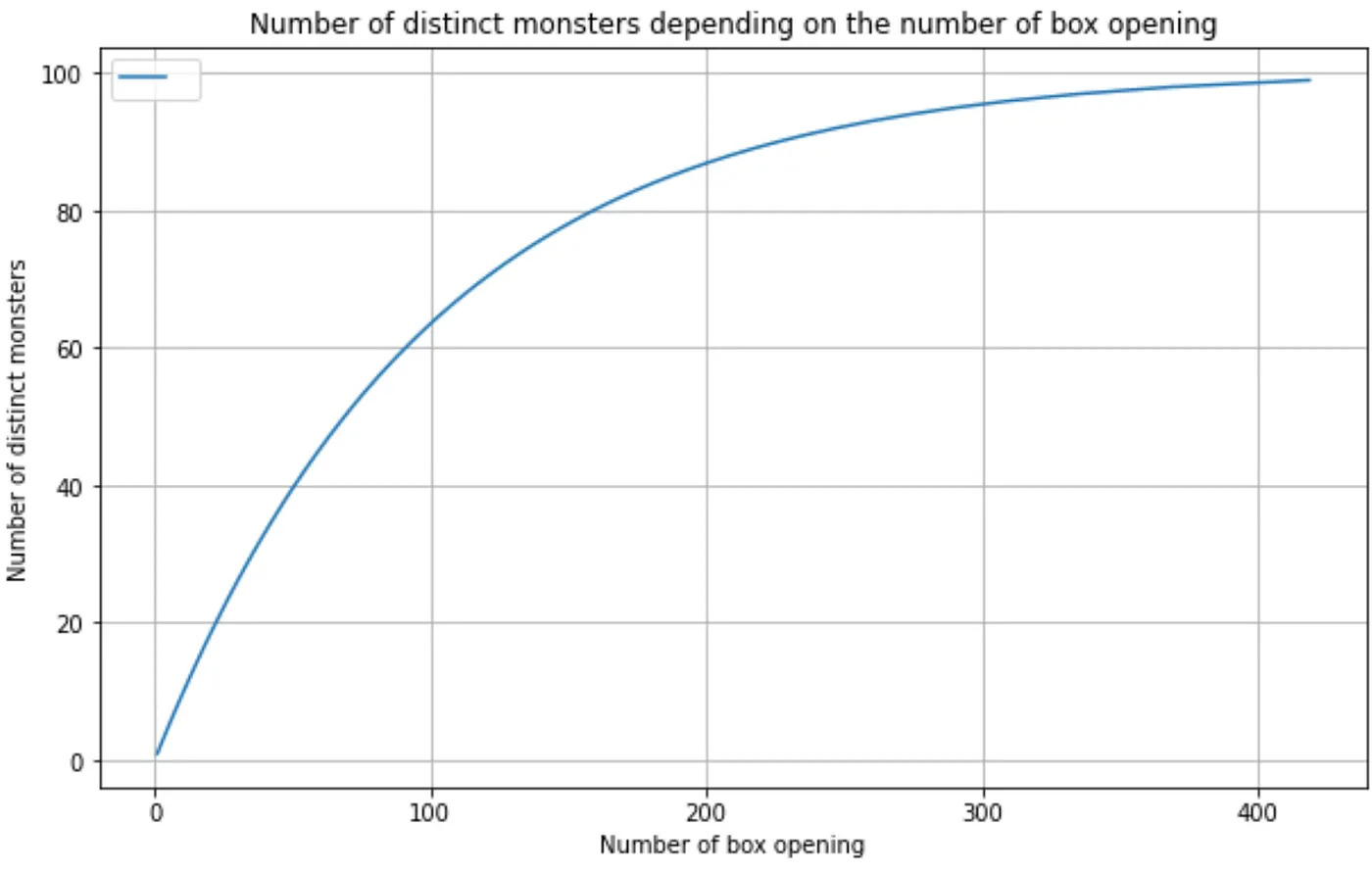
print("And to be sure to have all 100 distinct monsters we'd need to open on average {} boxes".format(int(openbox_depending_on_monster_np(100))))We can also plot the evolution of the number of our distinct monsters, depending on the number of box openings:
Show code
# Range of k values from 1 to 100
N = 100
k_values = np.arange(1, N)
# Compute the sum for each k
sum_results = [openbox_depending_on_monster_np(k) for k in k_values]
# Create the plot
plt.figure(figsize=(10, 6))
plt.plot(sum_results, k_values, label=' ')
plt.xlabel('Number of box openings')
plt.ylabel('Number of distinct monsters')
plt.title('Number of distinct monsters depending on the number of box openings')
plt.grid(True)
plt.legend()
plt.show()We can see that the more monsters we get, the harder it is to find new ones!
The opposite approach to the problem — a bit more complex
What if we approach the problem from the other side? How many distinct monsters do we get after opening k boxes?

Well, we could always look at our charts above and deduce that, but from a statistical point of view, it would look like this:
The probability that monster i has not been picked after k attempts is:
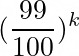
So the probability that monster i has been picked at least once is:
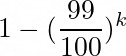
Given that each of the 100 monsters has the same probability of appearing, we can use the linearity of expectation to find the expected number of different monsters seen after k attempts:
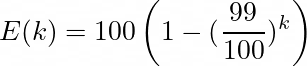
Show code
N = 100
def monster_depending_on_openbox(k):
total = N*(1-((N-1)/N)**k)
return total
print("So after opening 100 boxes, we'll have on average {} different monsters".format(int(monster_depending_on_openbox(100))))Non uniform distribution — quite more complex
Now, what happens if the probabilities of obtaining each monster are not uniform when opening a box? Let’s say we have 90 monsters with a probability of being found of 1/91 and 10 rare monsters with a probability of being found of 1/910.
How many box openings will it take to collect all 100 different monsters?
Well, the mathematical approach gets a bit more complicated, so we’ll venture into the world of simulation with Monte Carlo methods.
Monte Carlo methods
Monte Carlo methods are a type of computational algorithm used to solve problems through random sampling. We are going to simulate multiple series of box openings until we reach our target of unique monsters, and then we will see on average how many box openings we needed.

Show code
import numpy as np
# Define probabilities for each monster
probabilities = [1/91] * 90 + [1/910] * 10
#probabilities = [1/100] * 100 #we can do that if we want to simulate with uniform distribution
probabilities = np.array(probabilities) / sum(probabilities) # Normalize probabilities
# Number of total monsters
total_monsters = len(probabilities)
# Target number of unique monsters (we want to reach 100 of unique monsters)
target_unique_monsters = 100
# Function to simulate opening boxes until we reach the target
def simulate_boxes():
collected_monsters = set()
box_count = 0
while len(collected_monsters) < target_unique_monsters:
monster = np.random.choice(total_monsters, p=probabilities)
collected_monsters.add(monster)
box_count += 1
return box_count
# Number of simulations
num_simulations = 10000
results = [simulate_boxes() for _ in range(num_simulations)]
# Calculate the average number of boxes needed
average_boxes = np.mean(results)
print("To have all 100 distinct monsters we'd need to open on average {} boxes".format(int(average_boxes)))We can see how this addition of rarer monsters drastically increases the number of boxes we have to open to collect them all!
This number is an average, but each round of the simulation got a different number of box openings to get all the monsters. We can even visualize the distribution of the number of openings needed in each round of the simulation.
Show code
import matplotlib.pyplot as plt
# Plot the distribution of results from the simulations
plt.hist(results, bins=30, color='skyblue', edgecolor='black')
plt.title('Distribution of Boxes Needed to Collect all monsters')
plt.xlabel('Number of Boxes')
plt.ylabel('Frequency')
plt.grid(True)
plt.show()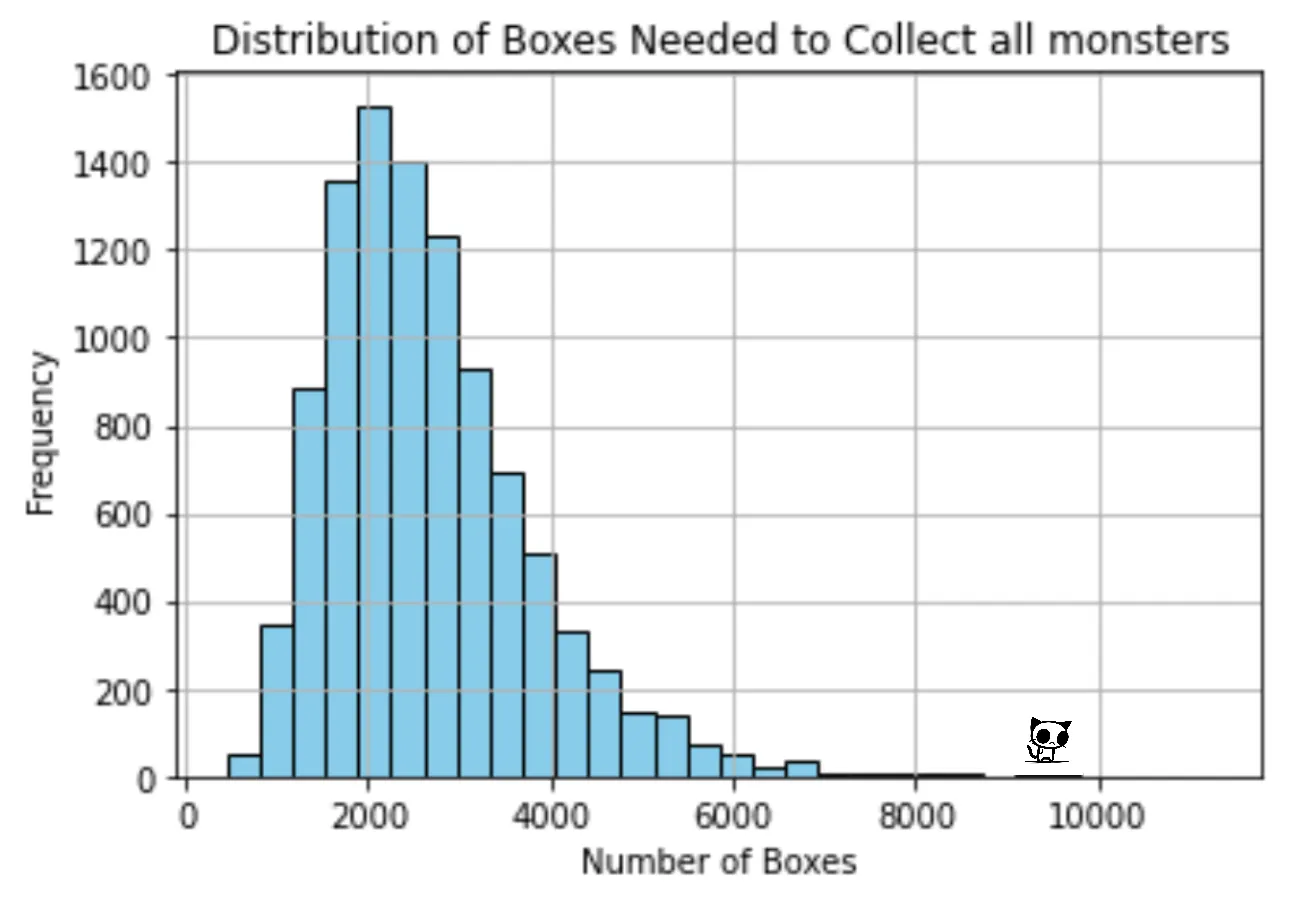
Conclusion
We’ve explored the Coupon Collector’s Problem from simple uniform distributions to complex scenarios with rare items. The math shows that collecting everything takes patience, especially when some items are much rarer than others.
Next time you open a pack or plan to collect something, remember: with math and persistence, even the most challenging collections can be completed!
